１アマ対策

無線工学メモ

無線工学から
測定器　電源
トランジスタ回路
ＦＥＴ回路

無線工学から†

このページは１アマ取得の際に必要とする計算式で面倒なものを簡素化するために考案した備忘録的なページです。

↑

合成インピーダンスの求め方†

複素数の計算を使えば普通の計算式のように扱える

↑

直列回路†

↑

並列回路†

↑

ログ計算の簡単な方法†

下記の表を覚えておくだけで面倒なログ計算はいらない

電力	3dB	6dB	9dB	10dB	12dB	15dB	18dB	24dB
倍数	2倍	4倍	8倍	10倍	16倍	32倍	64倍	128倍

電流電圧電界	6dB	12dB	18dB	20dB	24dB	30dB	36dB	42db
倍数	2倍	4倍	8倍	10倍	16倍	32倍	64倍	128倍

詳しい計算方法はログ計算の方法にある。

↑

共振問題†

↑

Ｌが固定で、Ｃが36％減った時にＦはどのくらい変化％するかを問う問題†

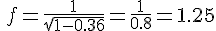$f=\frac{1}{\sqrt{1-0.36}}=\frac{1}{0.8}=1.25$ 　25％増加する

↑

共振周波数やＬやＣを簡単に求める方法†

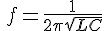有名な公式 $f=\frac{1}{2\pi\sqrt{LC}}$ から求めるのが基本だが、今回のＣＱ誌にあった簡単な計算方法でも求めることが出来る

Ｃ：ｐＦ　Ｆ：μＨ　ｆ：ＭＨｚ

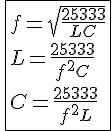
$\fbox{f=\sqrt{\frac{25333}{LC}}\\L=\frac{25333}{f^2C}\\C=\frac{25333}{f^2L}}$

共振Ｑ　　並列　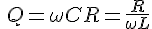 $Q=\omega{}CR=\frac{R}{\omega{}L}$

　　　　　直列　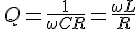 $Q=\frac{1}{\omega{}CR}=\frac{\omega{}L}{R}$

↑

共振時のＺについて†

並列　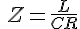　 $Z=\frac{L}{CR}$ 　非常に高いインピーダンスになる

並列　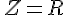　 $Z=R$ 　純抵抗のみの低い数値になる

↑

mufの求め方†

↑

muf（到達最大周波数）を求める†

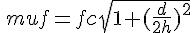公式では $muf=fc\sqrt{1+(\frac{d}{2h})^2}$ となる。

しかし、正割の法則を使えばもっと単純に計算できる。
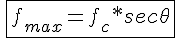
$\fbox{f_{max}=f_c*sec\theta}$

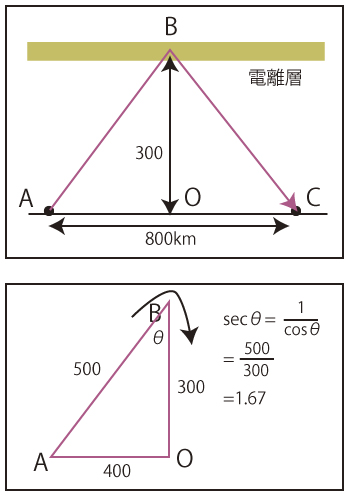
上図の場合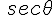 $sec\theta$ は1.67になる。これに発射する周波数Fcを乗算すれば良いだけである。

↑

直接波による通信可能距離†

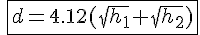
$\fbox{d=4.12(\sqrt{h_1}+\sqrt{h_2})}$

例えば同じ標高で障害物が何もない砂漠のような平らな場所に二人がハンディトランシーバーで通話使用とした場合を考えると、地上高約２メートルくらいだから
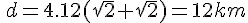
$d=4.12(\sqrt{2}+\sqrt{2})=12km$

空気中の散乱などを考慮に入れないと12kmの通話距離と考えられる。
実際には屈折や散乱などでもっと距離が伸びる。

↑

直接波と反射波による電界強度の計算†

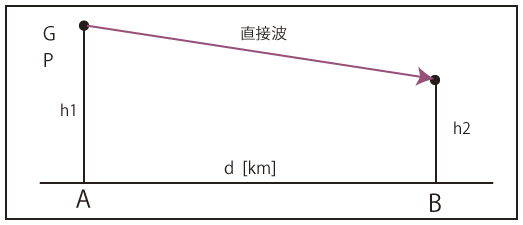
送信アンテナで相対利得Ｇ、Ｐワットで電波を発射したとき最大放射方向の距離ｄにおける電界強度Ｅは
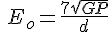$E_o=\frac{7\sqrt{GP}}{d}$ となります。
これから、Ａ点Ｂ点のアンテナ高、波長を入れたときの式は

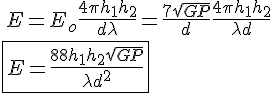
$E=E_o\frac{4\pi{}h_1h_2}{d\lambda}=\frac{7\sqrt{GP}}{d}\frac{4\pi{}h_1h_2}{\lambda{}d}\\\fbox{E=\frac{88h_1h_2\sqrt{GP}}{\lambda{}d^2}}$

となる

相対利得が6dBで地上高25mの送信アンテナに周波数150MHzで25Wの電力を供給して電波を発射したとき、最大放射方向で送受信間の距離が20kmの地点における受信電界強度は？
ただし、受信アンテナの地上高は20mとする

↑

測定器　電源†

↑

実効値、平均値、最大値†

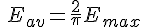平均値： $E_{av}=\frac{2}{\pi}E_{max}$ \\

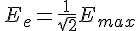実効値： $E_{e}=\frac{1}{\sqrt{2}}E_{max}$ \\

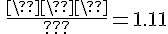
波高率： $\frac{\実\効\値}{平均値}=1.11$

↑

テスターの倍率抵抗†

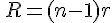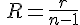
r:内部抵抗　n:倍率　　電圧計　 $R=(n-1)r$ 　　電流計　 $R=\frac{r}{n-1}$

↑

時定数†

ＲやＬ、Ｃの直列回路で直流電圧をかけたときに定常電圧の63.2％になるまでの時間を時定数という
$t=CR\\t=\frac{L}{R}$

↑

トランジスタ回路†

回路特性	エミッタ接地	ベース接地	コレクタ接地
入力インピーダンス	低い	低い	高い
出力インピーダンス	高い	高い	低い
電圧利得	大きい	大きい	１以下、ほぼ１
電流利得	大きい	１より小さい、ほぼ１	大きい
電力利得	大きい	エミッタ接地より小	エミッタ接地より小（電流利得は大だが電圧利得が１）
交流信号の位相	逆相	同相	同相
周波数特性	あまり良くない	良好（ミラー効果なし）	良好（ミラー効果なし）

↑

ＦＥＴ回路†

回路特性	ソース接地	ドレイン接地	ゲート接地
入力インピーダンス	高い	高い	低い
出力インピーダンス	負荷抵抗で決まる	負荷抵抗で決まる	高い
電圧増幅率	１より大きい	1より小さい
電流増幅率
位相

User名私コールサイン

パスワード最高信号強度

無線工学から†

合成インピーダンスの求め方†

直列回路†

並列回路†

ログ計算の簡単な方法†

共振問題†

Ｌが固定で、Ｃが36％減った時にＦはどのくらい変化％するかを問う問題†

共振周波数やＬやＣを簡単に求める方法†

共振時のＺについて†

mufの求め方†

muf（到達最大周波数）を求める†

直接波による通信可能距離†

直接波と反射波による電界強度の計算†

測定器　電源†

実効値、平均値、最大値†

テスターの倍率抵抗†

時定数†

トランジスタ回路†

ＦＥＴ回路†

おすすめ

最新の30件

１アマ対策

無線工学から†

合成インピーダンスの求め方†

直列回路†

並列回路†

ログ計算の簡単な方法†

共振問題†

Ｌが固定で、Ｃが36％減った時にＦはどのくらい変化％するかを問う問題†

共振周波数やＬやＣを簡単に求める方法†

共振時のＺについて†

mufの求め方†

muf（到達最大周波数）を求める†

直接波による通信可能距離†

直接波と反射波による電界強度の計算†

測定器 電源†

実効値、平均値、最大値†

テスターの倍率抵抗†

時定数†

トランジスタ回路†

ＦＥＴ回路†

おすすめ

最新の30件

測定器　電源†